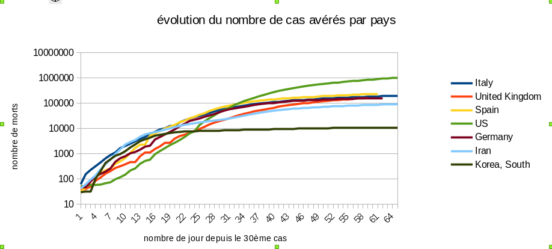
On retrouve dans l’article du monde1 suivant la propagation du virus dans LE monde ce genre de graphique représentant le nombre de cas avéré de covid-19 pour plusieurs pays
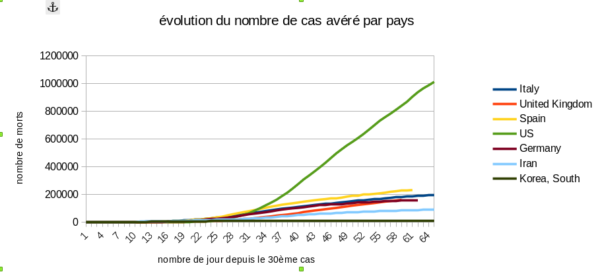
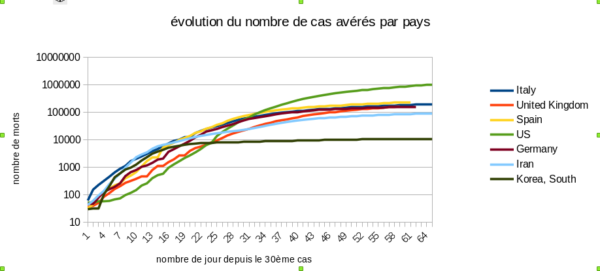
ATTENTION: une erreur de notre part s’est glissé dans la légende de l’axe des ordonnées de ces deux graphiques: il ne s’agit pas du nombre de mort.es, mais du nombre de cas avérés. On va corriger.
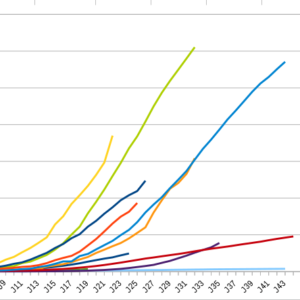
On peut donc observer deux types de graphiques, le premier appelé total et le second appelé rythme dans l’article. L’article nous met en garde : le mode « rythme » adopte une échelle logarithmique afin de mieux visualiser le rythme de chacun de ces foyers, là où le mode « total » utilise une échelle linéaire classique.
Si on est pas super à l’aise avec les maths, les mots logarithmique et linéaire ne sont pas forcément super aidant pour comprendre ce qu’il se passe. Dans l’article les graphiques en bâton ou comment faire disparaître des grévistes2 on expliquait qu’il fallait faire attention aux problèmes d’échelle, en effet on est pas forcé de faire commencer une échelle à 0 ce qui va influer sur la compréhension du graphique.
Et bien il est aussi possible de jouer sur la graduation du graphique : une échelle linéaire c’est une échelle normal, chaque fois qu’on monte d’une ligne on monte d’un certain nombre. Sur le premier graphique par exemple quand on monte d’une ligne on monte de 200.000.
Avec une échelle logarithmique, chaque fois qu’on monte d’une ligne on multiplie par un certain nombre. Sur le deuxième graphique quand on monte d’une ligne, on multiplie par 10.
Les deux graphiques représentent bien les même donnés, le premier peut avoir un coté alarmiste, notamment pour les états-unis, quand le second est plutôt rassurant avec une impression que ça se tasse.
Vous vous demandez sûrement : mais pourquoi donc représenter les donnés d’une manière aussi bizarre ?
Les échelles logarithmiques permettent de représenter sur un même graphique des donnés avec des ordres de grandeur très différents : dans le premier graphique les courbes sont indiscernables jusqu’au 30ème jour à peu près alors que dans le second elle reste lisible. Et le nombre de cas au états-unis n’est « que » cinq fois supérieur aux autres pays observé, si on fait apparaître sur un graphique une valeur montant cent fois plus haut que d’autres, aucune valeur n’est plus lisible.
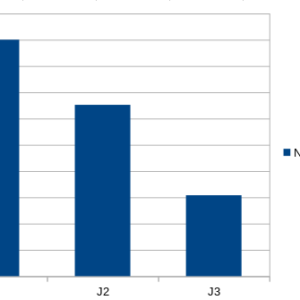
supposons que le nombre d’adhérent au ceméa double chaque année et qu’il y ai 3 adhérents la première année :
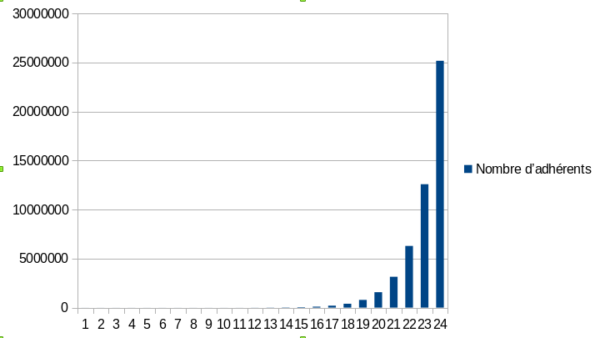
On remarque d’abord que c’est une estimation plutôt optimiste avec plus de 25 millions d’adhérents dans 24 ans mais surtout que c’est une très mauvaise représentation puisqu’on ne peut lire correctement que 3 bâtons du graphique.
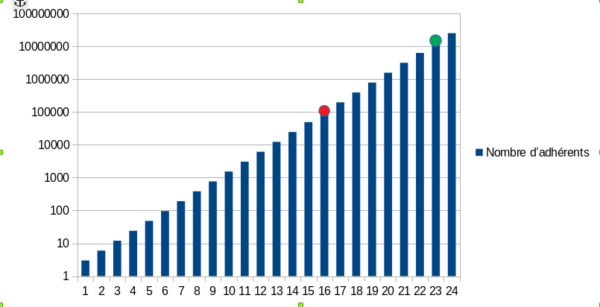
On arrive beaucoup mieux à lire les donnés du graphique avec une représentation logarithmique.
Ce genre de graphique permet donc de mettre en avant les ordres de grandeurs différents, deux donnés éloignés sur le graphique sont très éloignés dans la réalité : par exemple le point rouge représente le nombre d’adhérents à la 16ème année et le point vert le nombre d’adhérent à la 23ème année, ils sont éloignés de deux « étages », ils ne représente donc pas le même ordre de grandeur, 10.000.000 pour le point vert et 100.000 pour le point rouge deux valeurs très éloignées.
Par contre, ce genre de graphique ne permet pas de bien faire apparaître les différences entre deux valeurs du même ordre de grandeur : le point vert est à peu près sur la ligne des 10.000.000 mais représente en fait 12.500.000. Deux nombres du même ordre de grandeur mais avec une différence pourtant non négligeable.
Utilisation frauduleuse
Il est tout à fait possible d’utiliser cet effet de tassement pour induire une fausse compréhension des donnés. Par exemple dans ce graphique que j’ai fait avec des vrais donnés, on voit bien que tous les ménages gagnent à peu près le même revenu dans l’UE.
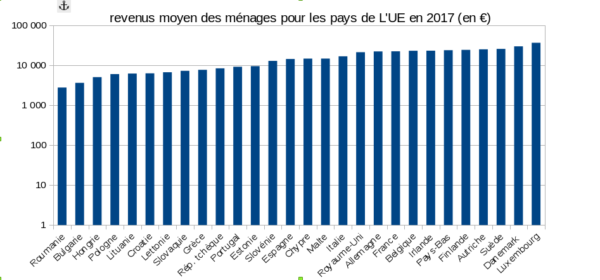
et comme vous vous en doutez la réalité est toute autres, les ménages luxembourgeois gagnent en moyenne plus de 13 fois plus que les ménages roumains3 comme on le voit beaucoup mieux sur un graphique avec une échelle adaptée.
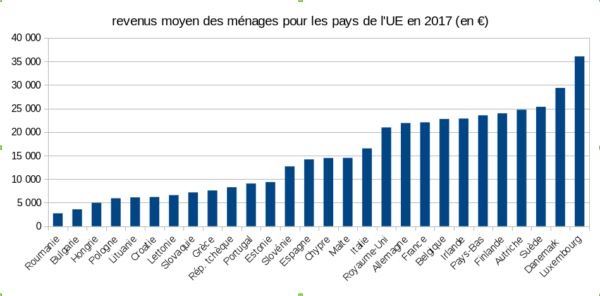
Les échelles chelou
Comme on adore le monde et leurs articles, on a continué de fouiller et on a trouvé ce graphique4
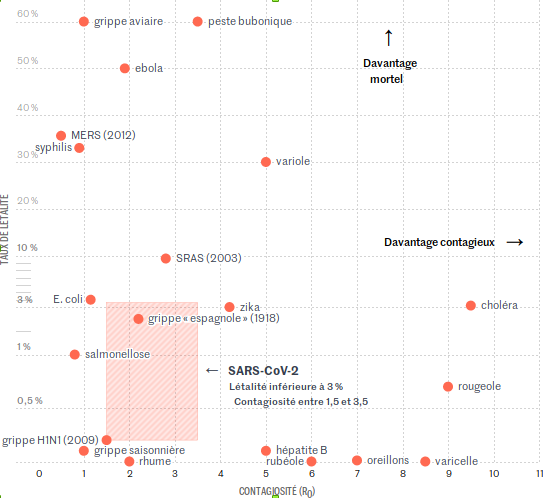
Le taux de létalité en ordonnée (l’axe vertical) représente la proportion du nombre de mort d’une maladie par rapport au nombre d’infectés, par exemple 60% des gens atteint de la peste bubonique en sont mort (RIP). La contagiosité en abscisse (l’axe horizontal) représente le nombre moyen de personne infectée par une personne infectée elle même, par exemple une personne atteinte de la peste bubonique infecte en moyenne 3 personnes et demi.
De nouveau le site nous met en garde : Entre 0 % et 10 %, nous avons étendu l’échelle afin de rendre le graphique plus lisible, du fait du grand nombre de maladies situées entre ces bornes de mortalité.
En effet si on regarde l’échelle en ordonné elle est assez inhabituelle, il n’ont pas simplement étendu l’échelle de manière uniforme, ils l’ont étendu selon leurs convenances c’est à dire les deux premiers paliers représentent 0,5%, le suivant 2%, le troisième 7% et les autres représentent 10%.
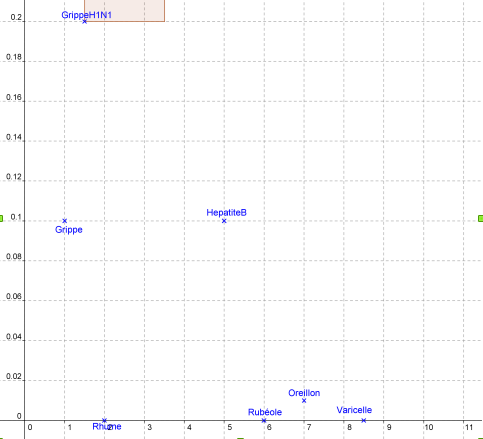
Si on représente les mêmes donnés en prenant une échelle linéaire on obtiens un graphique comme celui ci
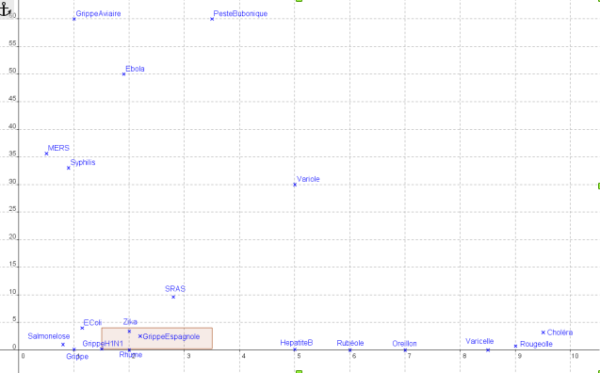
Effectivement on ne voit plus très bien la différence entre le taux de létalité de la Rubéole et celle des oreillons (respectivement 0% et 0,01%) par contre ça permet de bien voir que la salmonelose est 10 fois moins létal que le SRAS ou que le SRAS est 10 fois moins létal qu’ébola et non pas deux fois moins comme on pourrait croire à première vue dans le premier graphique.
Dans le graphique « zoomé » du monde, le carré rouge représentant le Sars-Cov2 est énorme ce qui fait penser à un fort taux de létalité, le fait qu’il soit plus haut que large peut jouer aussi dans cette impression de hauteur. Dans le graphique remis à l’échelle il est beaucoup plus petit (et donc moins haut que large) et est donc moins impressionnant.
Le but du graphique étant de comparer la létalité et la contagiosité du Sars-Cov2 avec d’autre virus, un tel agrandissement ne me semble pas vraiment utile. On réussi mieux la comparaison avec les virus du haut du graphique et il n’y a pas d’intérêt ici à comparer entre eux les virus dont la létalité est proche de zéro
Si vraiment le but est de bien comprendre le bas du graphique, un deuxième graphique à une autre échelle me paraît moins trompeur en termes d’interprétation :
Sources :
2 ( https://covid19.cemea-pdll.org/1-2-les-graphiques-en-baton-ou-comment-faire-disparaitre-des-grevistes/ )
3 (https://www.insee.fr/fr/statistiques/4277695?sommaire=4318291 )